The mechanisms for enhancing learning and human learning are very similar, and DeepMind has applied enhanced learning to scenarios such as AlphaGo and Atari games. The collaborative research of Afan Research Institute, University of Electronic Science and Technology and Peking University first proposed an automatic solver for arithmetic application based on DQN (Deep Q-Network), which can transform the problem-solving process of application questions into Markov decision The process, and the BP neural network's good generalization ability, storage and approximation enhances the Q-value of the state-action pair in learning. Experiments show that the algorithm performs well in the standard test set and increases the average accuracy by nearly 15%.
Research Background
The research history of Automatic Solving Mathematical Application Questions (MWP) dates back to the 1960s and has continued to attract researchers' attention in recent years. The automatic solution of applied mathematics first maps human-readable sentences into machine-understandable logical forms and then makes inferences. This process can't be solved simply by pattern matching or end-to-end classification technology. Therefore, designing an automatic problem solver with semantic understanding and reasoning ability has become an indispensable step in the road to general artificial intelligence.
For the mathematics application solver, given a mathematical application text, you can't simply train it end-to-end by means of text question and answer, so that you can directly get the answer, but you need to use text processing and numerical reasoning to get It solves the expression and calculates the answer. Therefore, this task not only involves a deep understanding of the text, but also requires the solver to have strong logical reasoning ability, which is also a difficult point and focus in the study of natural language understanding.
In recent years, researchers have designed algorithms from different angles and written solving systems to try to solve mathematical problems automatically, including template-based methods, statistical-based methods, expression tree-based methods, and deep learning-based generation. The method of the model. At present, solving the relevant fields of mathematics application questions, there are not enough training data sets, the robustness of the solution algorithm is not strong, the solution efficiency is not high, and the solution effect is not good. Because the mathematics itself requires sufficient understanding of natural language, it has strong reasoning ability for numbers, semantics and common sense. However, most of the solving methods are subject to more manual intervention, the versatility is not strong, and with the increase of data complexity. Most of the algorithms solve the effect sharply, so it is difficult and very important to design an automatic solver with good performance and effect.
Related work
Arithmetic Application Solver:
As an early attempt, the method based on verb classification and state transition reasoning can only solve the problem of addition and subtraction. In order to improve the ability to solve, the label-based method is designed with a large number of mapping rules, which map variables and numbers into logical expressions for reasoning. Due to excessive manual intervention, it is difficult to expand.
Based on the expression tree method, try to identify the relevant numbers, and classify the operators between the pairs of numbers, and construct an expression tree that can be solved from the bottom up. In addition, some ratio units and the like are considered to further ensure the correctness of the constructed expression. Based on the equation tree approach, a more violent approach is adopted, enumerating all possible equation trees through integer linear programming. The tree-based approach is faced with an exponential increase in the number of digits as the number of digits increases or decreases.
Equations Application Solver:
For the solution of the equations application, the current method is mainly based on the template. The method needs to classify the text into a predefined system of equations, inferring the arrangement of the unknown slots by artificial features, and filling the identified numbers and related noun units in the slots. The template-based approach has a high dependence on data. When the number of questions corresponding to the same template is reduced, or the complexity of the template is increased, the performance of this method will drop dramatically.
The main contributions of this paper are as follows:
The first attempt to use deep-enhanced learning to design a general mathematical problem-solving framework
For the application problem scenario, the corresponding state, action, reward function, and network structure of the deep Q network are designed.
The proposed method is validated on the main arithmetic application dataset, and good results are obtained in the solution efficiency and solution effect.
An Introduction
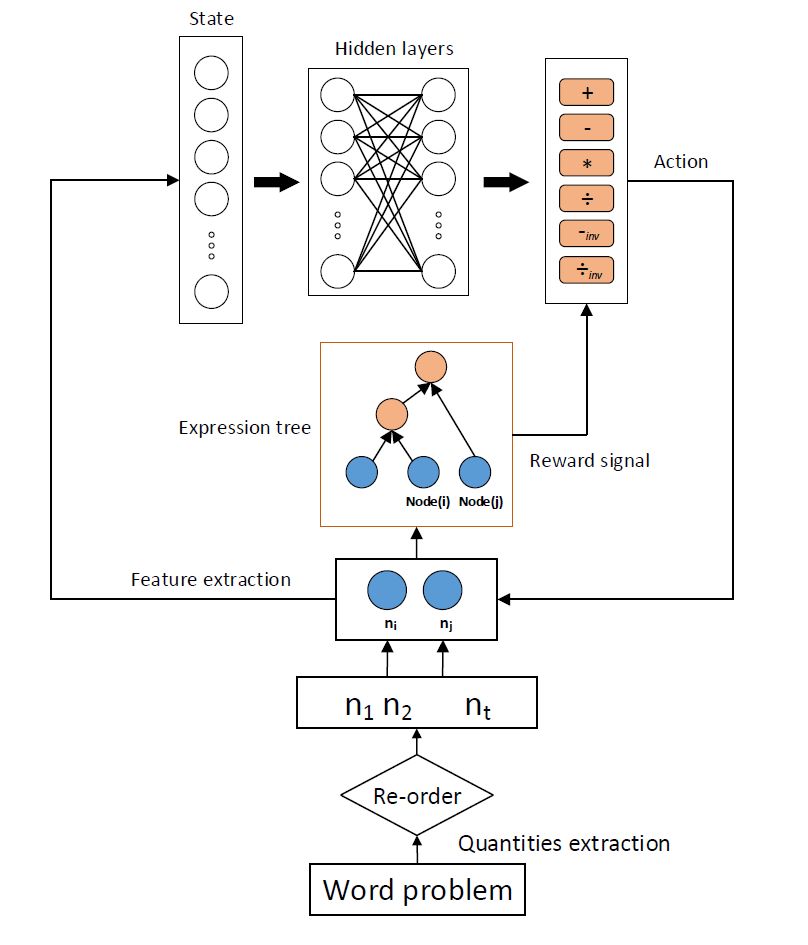
Mathematical application solver based on depth Q network
The framework presented in this paper is shown in the figure above. To give a mathematical application problem, firstly use the digital pattern to extract the relevant numbers used to construct the expression tree, and then adjust the extracted related numbers according to the rules of reordering, for example, for "3+4*5", We want to calculate 4*5 first, where the number 5, the corresponding text segment is "5 yuan per hour", obviously the unit of the number "5" here is "yuan/hour", when the unit of the number "4" is "Hour", the unit of the number "3" is "yuan". In this case, adjust 4 and 5 to the front of the sequence of numbers, and then, construct the expression from the bottom up with the sequence of numbers that have been sorted. First, according to the respective information of the number "4" and the number "5", the information between each other, and the relationship with the problem, the corresponding features are extracted as the state in the enhanced learning component.
Then, this feature vector is used as the input of the forward neural network in the depth Q network, and the six actions of "+", "-", reverse "-", "*", "/", and reverse "/" are obtained. The Q value, according to epsilon-greedy, selects the appropriate operator as the current action, and the numbers "4" and "5" start to construct the expression tree according to the currently taken action. Next, repeat the process of the previous step according to the number "4" and the number "3", or the number "5" and the number "3", and construct the expression tree by the smallest common element ancestor of the operator number. Until there are no more relevant figures, the end of the tree. The design of the various components of the deep Q network will be detailed later.
status:
For the current pair of numbers, based on the number pattern, extract a single number, a pair of numbers, a three-category feature related to the question, and whether the two numbers have participated in the construction of the expression tree as the current state. Among them, a single number, a number pair, and a problem-related three types of features help the network to select the correct operator as the current action; whether the number participates in the construction of the expression tree, implying that the current number pair is in the current expression tree The hierarchical location.
action:
Because this article deals with simple arithmetic application problems, only consider the addition, subtraction, multiplication, and division of the four operations. In the process of building a tree, for addition and multiplication, the different numerical order between the two numbers will not affect the calculation result, but the different order of subtraction and division will lead to different results. Since we implement the order in which the numbers are determined, it is necessary to add two operations, inverse subtraction and inverse division. Therefore, the total of addition, subtraction, multiplication, division, inverse subtraction and division 6 operators are required to learn as a depth Q network.
Reward function:
In the training phase, the depth Q network selects the correct action based on the current two numbers, and gets the correct operator. The environment feeds back a positive value as a reward, otherwise it feeds back a negative value as a penalty.
Parameter learning:
This paper uses a two-layer forward neural network for the depth Q network to calculate the expected Q value. The parameter θ of the network will update the learning according to the reward function of the environmental feedback. This article uses empirical replay memory to store transfers between states and batch sampling from the experience replay memory.  Used to update network parameters. The loss function of the model is as follows:
Used to update network parameters. The loss function of the model is as follows:
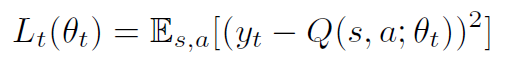
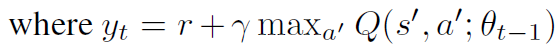
The gradient value of the loss function is used to update the parameters to narrow the gap between the predicted Q value and the desired target Q value. The formula is as follows:
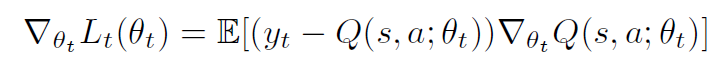
The algorithm flow is as follows:

experiment
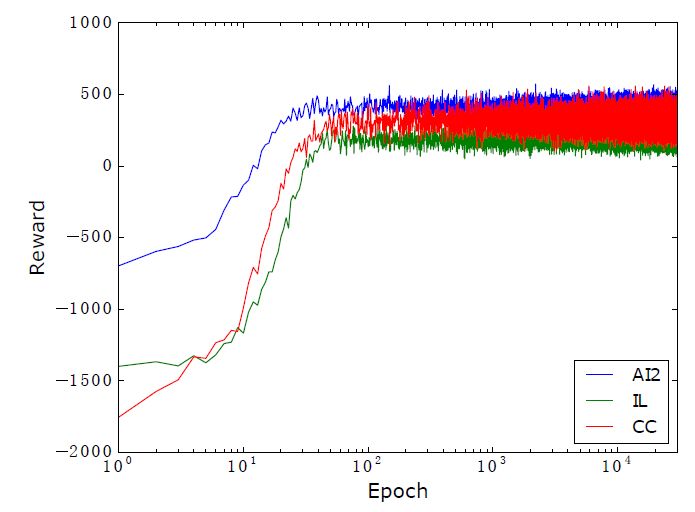
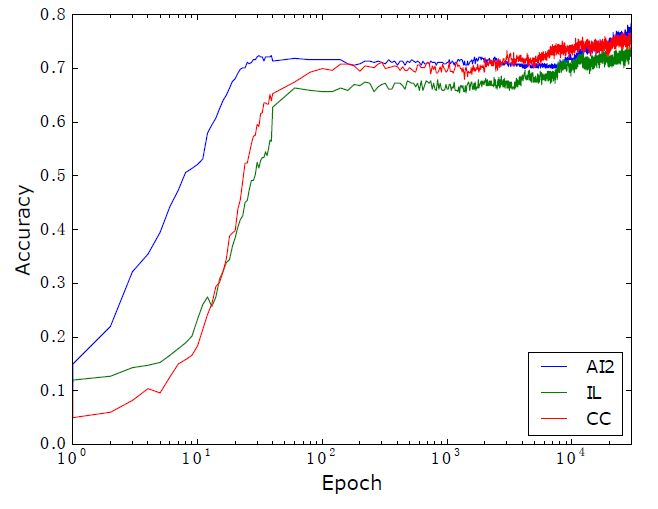
In this paper, three arithmetic application data sets of AI2, IL and CC are used to carry out experiments. Among them, AI2 has 395 questions, and the title contains irrelevant numbers, which only involve addition and subtraction. IL has 562 questions. The title contains irrelevant numbers. It only involves addition, subtraction, multiplication and division. The CC has 600 questions. The title does not contain irrelevant numbers. It involves two steps of addition, subtraction, multiplication and division.
The accuracy of the three data sets is as follows:
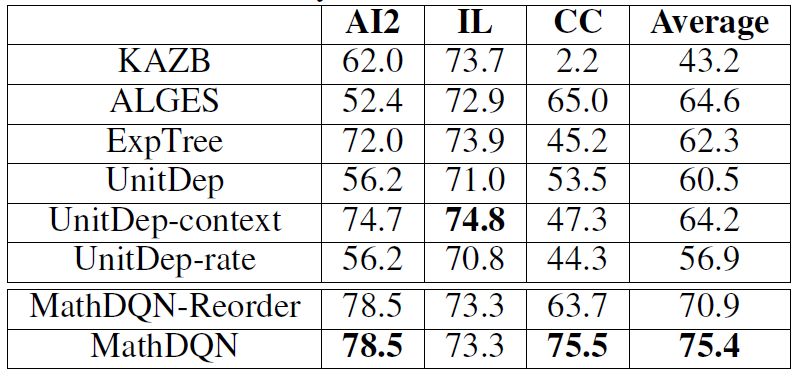
Observing the above experimental results, it is found that the proposed method achieves the best results on the AI2 and CC data sets. ALGES performed very well on IL, but performed poorly on the AI2 and CC datasets, which proves that our approach is more versatile. The unit dependency graph proposed by UnitDep has no obvious effect on the AI2 dataset with only addition and subtraction. The added Context feature has obvious effect on the CC dataset, but the effect on the AI2 dataset is significantly reduced. The limitations of artificial features. For the method proposed in this paper, the reordering is obvious on the CC dataset. Since AI2 only has addition and subtraction operations, IL only involves single-step operations, so the effect is unchanged on these two datasets.
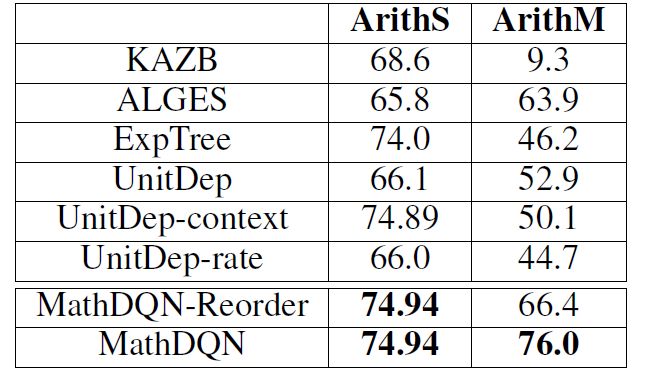
In addition, this paper also made single-step and multi-step breakpoint analysis. The experimental results show that the proposed method performs very well in multiple steps. The experimental results are as follows:
The running time is as follows:
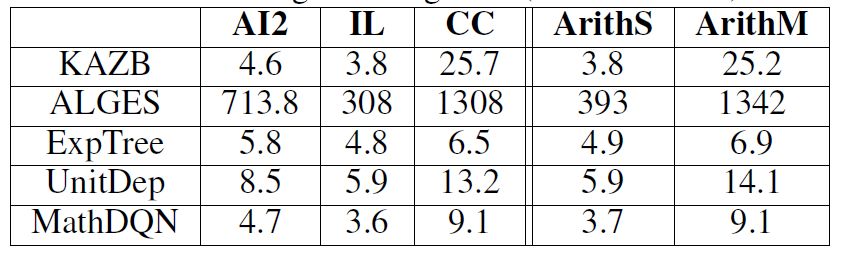
Observing the time required to solve a single problem, we can find that the data set CC of the multi-step operation is obviously more expensive in time. ALGES takes the longest time to enumerate all possible candidate trees. The method proposed in this paper is second only to the SVM operator, and the associated digital classification of ExpTree.
The average reward and accuracy trend is as follows:
to sum up
In this paper, an enhanced learning framework for solving mathematical problems is proposed for the first time. The efficiency and solution effect on the benchmark data show good results.
In the future, we will continue to learn along the depth and enhance the learning line to design an automatic solver for math problems to avoid excessive artificial features. At the same time, try to solve the equations application problem on a larger and more diverse data set.
ZGAR AZ Vape Pods 5.0
ZGAR electronic cigarette uses high-tech R&D, food grade disposable pod device and high-quality raw material. All package designs are Original IP. Our designer team is from Hong Kong. We have very high requirements for product quality, flavors taste and packaging design. The E-liquid is imported, materials are food grade, and assembly plant is medical-grade dust-free workshops.
From production to packaging, the whole system of tracking, efficient and orderly process, achieving daily efficient output. WEIKA pays attention to the details of each process control. The first class dust-free production workshop has passed the GMP food and drug production standard certification, ensuring quality and safety. We choose the products with a traceability system, which can not only effectively track and trace all kinds of data, but also ensure good product quality.
We offer best price, high quality Pods, Pods Touch Screen, Empty Pod System, Pod Vape, Disposable Pod device, E-cigar, Vape Pods to all over the world.
Much Better Vaping Experience!

Pods, Vape Pods, Empty Pod System Vape,Disposable Pod Vape Systems
ZGAR INTERNATIONAL(HK)CO., LIMITED , https://www.zgarpods.com