The optimization method has always been a very important part of machine learning and the core algorithm of the learning process. Adam has received widespread attention since it was proposed in 14 years, and the citations of the paper have reached 10047. However, since last year, many researchers have found that the convergence of the Adam optimization algorithm is not guaranteed. The best paper of ICLR 2017 also focuses on its convergence. In this article, the author found that most of the Adam implementations of deep learning libraries have some problems, and implemented a new AdamW algorithm in the fastai library. According to some experiments, the author stated that this algorithm is currently the fastest way to train neural networks.
Adam roller coaster
The Adam optimizer journey can be said to be a roller-coaster style. The optimizer was launched in 2014. It is essentially a simple and intuitive idea: Since we clearly know that certain parameters need to move faster and farther, why should each parameter follow the same learning rate? Because the square of the recent gradient tells us how much signal each weight can get, we can divide by this to ensure that even the dullest weight has a chance to shine. Adam accepted this idea and added a standard method in the process, which resulted in the Adam optimizer (with slight adjustments to avoid deviations in early batches)!
When it was first published, the deep learning community was excited about some charts from the original paper (as shown below):
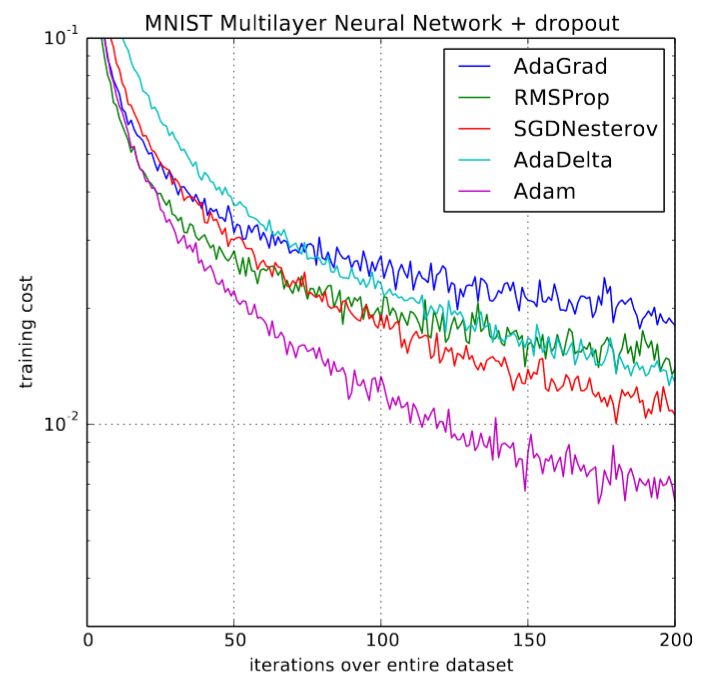
Comparison of Adam and other optimizers
Training speed increased by 200%! "Overall, we found that Adam is very robust and widely applicable to various non-convex optimization problems in the field of machine learning," the paper concluded. That was the golden age of deep learning three years ago. However, things did not develop in the direction we expected. There are few research articles using Adam training model. New research has obviously inhibited its application. In several experiments, it has been shown that SGD+momentum may perform better than the complex Adam. When the 2018 fast.ai course started, poor Adam was removed from the earlier course.
But by the end of 2017, Adam seemed to be reborn again. Ilya Loshchilov and Frank Hutter pointed out in their paper "Fixing Weight Decay Regularization in Adam" that the weight decay implemented by each library on Adam seems to be wrong, and proposed a simple method (they call it AdamW ) To fix it. Although the results are slightly different, they did give some encouraging graphs similar to the one below:

Comparison of Adam and AdamW
We hope that people will regain their enthusiasm for Adam, because some of the early results of the optimizer seem to be reproducible. But things backfired. In fact, the only deep learning framework that uses it is fastai encoded with Sylvain. Due to the lack of a broad framework available, everyday practitioners can only stick to the old and unusable Adam.
But this is not the only problem. There are many obstacles ahead. Two papers pointed to obvious problems with Adam’s proof of convergence, although one of them proposed an amendment called AMSGrad (and won the "Best Paper" award at the prestigious ICLR conference). But if we have learned anything from this brief history of the most dramatic life (at least by optimizer standards), it is that nothing is what it looks like on the surface. Indeed, PhD student Jeremy Bernstein pointed out that the so-called convergence problem is actually just a sign of improper selection of hyperparameters, and perhaps AMSGrad cannot solve the problem. Filip Korzeniowski, another PhD student, showed some early results that seemed to support the frustrating view of AMSGrad.
Start the roller coaster
So what should those of us who only want to train accurate models quickly? We choose to resolve this dispute with the method that has been used to resolve scientific debates for hundreds of years-scientific experiments! All the details will be presented later, but first let's look at the rough results:
After proper tuning, Adam can really be used! We got the latest results in terms of training time in the following tasks:
Train CIFAR10 on only 18 epochs or 30 epochs with increased testing time until its accuracy rate exceeds 94%, such as the DAWNBench competition;
Adjust the parameters of Resnet50 until its accuracy on the Stanford car data set reaches 90%, and only needs to train 60 epochs (600 epochs were required to achieve the same accuracy before);
Training an AWD LSTM or QRNN from scratch, after 90 epochs (or 1 and a half hours training on a GPU), its perplexity reached the current optimal level on Wikitext-2 (the previous LSTM required 750 epochs, QRNN 500 epochs are required).
This means that we have seen superconvergence using Adam! Superconvergence is a phenomenon that occurs when training neural networks with a high learning rate. It means that half of the training process is saved. Before AdamW, it took about 100 epochs to train CIFAR with an accuracy of 10 to 94%.
Compared with the previous work, we found that as long as the adjustments are made properly, Adam can achieve as good accuracy as SGD+Momentum on every CNN image problem we have tried, and it is almost always faster.
The suggestion that AMSGrad is a bad "solution" is correct. We have always found that AMSGrad does not achieve higher gains in accuracy (or other related indicators) than ordinary Adam / AdamW.
When you hear people say that Adam's generalization performance is not as good as SGD+Momentum, you will basically find that the hyperparameters they choose for their models are not good. Usually Adam needs more regularization than SGD, so when switching from SGD to Adam, make sure to adjust the regularization hyperparameters.
Article structure:
1. AdamW
Understanding AdamW
Implement AdamW
AdamW experiment and AdamW-ish
2. AMSGrad
Understand AMSGrad
Achieve AMSGrad
Results of AMSGrad experiment
3. Full result chart
AdamW
Understanding AdanW: Weight decay and L2 regularization
L2 regularization is a classic method to reduce overfitting. It adds a penalty term consisting of the sum of the squares of the weight of the model to the loss function, and multiplies it by specific hyperparameters to control the penalty. All the equations in this article are expressed in Python, NumPy and PyTorch styles:
final_loss = loss + wd * all_weights.pow(2).sum() / 2
Among them, wd is the hyperparameter we set to control the punishment. This can also be called weight decay, because every time the original SGD is used, it is equivalent to updating the weights using the following equation:
w = w-lr * w.grad-lr * wd * w
Among them, lr represents the learning rate, w.grad represents the derivative of the loss function with respect to w, and the following wd * w represents the derivative result of the penalty term with respect to w. In this equation, we will see that every update will subtract a small part of the weight, which is the source of "decay".
All the libraries reviewed by fast.ai use the first form. In practice, almost all algorithms are implemented through gradient wd*w, rather than actually changing the loss function. Because we don't want to add extra calculations to correct the loss, especially when there are other simple methods.
Since they are the same expression, why do we need to distinguish between these two concepts? The reason is that they are only equivalent to the original SGD, and when we add momentum or use complex optimization methods like Adam, L2 regularization (the first equation) and weight decay (the second equation) will be very Big difference. In the rest of this article, we discuss the weight decay referring to the second equation, and discussing L2 regularization is the first classic way.
As follows, in SGD with momentum, L2 regularization and weight decay are not equivalent. L2 regularization will add wd*w to the gradient, but now the weight is not directly subtracted from the gradient. First we need to calculate the moving average:
moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)
Then the weight can be updated by subtracting the moving average multiplied by the learning rate. So the regularization involved in the w update is lr* (1-alpha)*wd * w plus the combination of the previous weights already in moving_avg.
Therefore, the update method of weight attenuation can be expressed as:
moving_avg = alpha * moving_avg + (1-alpha) * w.grad w = w-lr * moving_avg-lr * wd * w
We can observe that subtracting the regularization part from w is different in the two methods. When we use the Adam optimizer, the weight attenuation may be more different. Because the L2 regularization in Adam needs to add wd*w to the gradient, calculate the moving average of the gradient and its square, and then update the weight. However, the weight decay method simply updates the weights and subtracts a point from the weights each time.
Obviously these are two different methods. After conducting experiments, Ilya Loshchilov and Frank Hutter suggested that we should use the weight decay method in the Adam algorithm instead of the L2 regularization implemented in the classic deep learning library.
Implement AdamW
So how can we implement the AdamW algorithm? If you are using the fastai library, you can simply add the parameter use_wd_sched=True when using the fit function:
learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)
If you prefer the new training API, you can use the parameter wd_loss=False in each training phase:
phases = [TrainingPhase(1, optim.Adam, lr, wds=1-e4, wd_loss=False)]learn.fit_opt_sched(phases)
The following is a brief overview of how fastai implements AdamW. In the step function of the optimizer, we only need to use the gradient to correct the parameter, not the value of the parameter itself (except for the weight decay, we will handle it externally). Then we can simply implement weight decay before the optimizer, but this still needs to be done after calculating the gradient, otherwise it will affect the value of the gradient. So in the training loop, we must determine where to calculate the weight attenuation.
loss.backward()#Do the weight decay here!optimizer.step()
Of course, the optimizer should set wd=0, otherwise it will do some L2 regularization, which is what we don't want to see. Now in the position of weight decay, we can write a loop statement on all the parameters, and adopt the weight decay update in turn. And our parameters should be stored in the optimizer's dictionary param_groups, so this loop should be expressed as the following statement:
loss.backward()for group in optimizer.param_groups(): for param in group['params']: param.data = param.data.add(-wd * group['lr'], param.data)optimizer. step()
Results of the AdamW experiment: can it really work?
We first tested on computer vision problems and the results were very good. Specifically, Adam and L2 regularization achieved an average accuracy of 93.96% in 30 epochs, and exceeded 94% in one of two. We chose 30 epochs because the 1cycle strategy and SGD can achieve 94% accuracy. When we use Adam and the weight decay method, we continue to obtain an accuracy rate of 94% to 94.25%. For this reason, we found that the optimal beta2 value when using the 1cycle strategy is 0.99. We regard the beta1 parameter as momentum in SGD, which means that the growth of its learning rate decreases from 0.95 to 0.85, and then increases to 0.95 as the learning rate decreases.
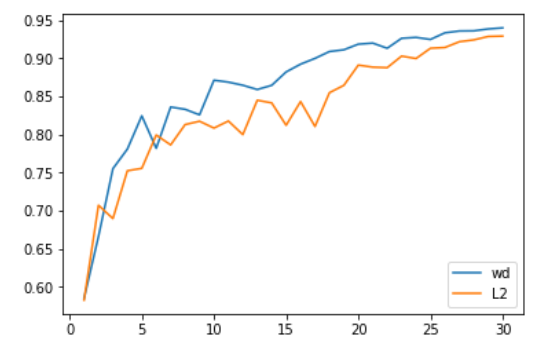
L2 regularization or weight decay accuracy
What’s more impressive is that using the increase in test time (that is, taking the average of the prediction on an image in the test set and its four versions with increased data), we can achieve 94% accuracy in just 18 epochs (93.98% on average)! With simple Adam and L2 regularization, more than 94% will occur every 20 attempts.
One thing to consider in these comparisons is that changing the regularization method will change the optimal value of the weight decay or learning rate. In our tests, the best learning rate for L2 regularization is 1e-6 (the maximum learning rate is 1e-3), and the best value for weight decay is 0.3 (the learning rate is 3e-3). In all our tests, the difference in order of magnitude is very consistent, mainly because the L2 regularization is effectively divided by the average norm of the gradient (relatively low), and the learning rate of Adam is quite small (so the weight decay update requires Stronger coefficient).
So, weight decay is always better than Adam's L2 regularization? We have not found a significantly worse situation, but neither transfer learning problems (such as the fine-tuning of Resnet50 on the Stanford car dataset) nor RNNs, it has not given better results.
AMSGrad
Understand AMSGrad
AMSGrad was introduced in a recent article by Sashank J. Reddi, Satyen Kale and Sanjiv Kumar. By analyzing the proof of the convergence of the Adam optimizer, they found an error in the update rule, which may cause the algorithm to converge to the next advantage. They designed a theoretical experiment to show how Adam failed, and proposed a simple solution. The heart of the machine has also analyzed this best paper from the adaptive learning rate algorithm: Beyond Adam.
In order to better understand the errors and solutions, let's take a look at Adam's update rules:
avg_grads = beta1 * avg_grads + (1-beta1) * w.gradavg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)w = w-lr * avg_grads / sqrt(avg_squared)
We just skipped the bias correction (useful for the beginning of training) and focused on the main points. The author found that the errors in Adam's proof of convergence are:
lr / sqrt(avg_squared)
This is our step towards the average gradient, which is gradually reduced during training. Since the learning rate is often constant or decreasing, the solution proposed by the author is to track their maximum value by adding another variable, thereby forcing the amount of avg_square to increase.
Achieve AMSGrad
The related article won an award in ICLR 2018 and is very popular, and it has been implemented in two major deep learning libraries-PyTorch and Keras. So, we only need to pass in the parameter amsgrad = True.
avg_grads = beta1 * avg_grads + (1-beta1) * w.gradavg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)max_squared = max(avg_squared, max_squared)w = w-lr * avg_grads / sqrt(max_squared)
AMSGrad experiment result: a lot of noise is useless
The results of AMSGrad are very disappointing. In all experiments, we found that it did not help at all. Even though the minimum value found by AMSGrad is sometimes slightly lower than the minimum value reached by Adam (in terms of loss), its metrics (accuracy, f_1 score...) are always worse in the end (see the table in the introduction for details).
The proof of the Adam optimizer's convergence in deep learning (because it addresses convex problems) and the errors they find in it are important for synthetic experiments that have nothing to do with real-world problems. Actual tests show that when these avg _ square gradients are to be reduced, doing so can get the best results.
This shows that even if focusing on the theory helps to get some new ideas, there is nothing to replace experiment (and a lot of experiments!) to ensure that these ideas actually help practitioners train better models.
Appendix: All results
Train CIFAR10 from scratch (the model is Wide-ResNet-22, the following is the average result of the five models):

Use the standard head introduced by the fastai library to fine-tune the Resnet 50 on the Stanford car data set (train the head for 20 epochs before thawing, and train 40 epochs with different learning rates):

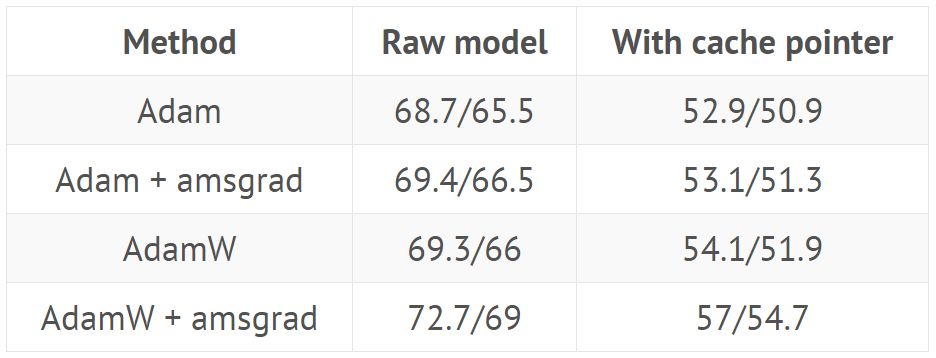
Use hyperparameters from GitHub (https://github.com/salesforce/awd-lstm-lm) to train AWD LSTM (the results show the perplexity of the validation/test set with or without cache pointers):
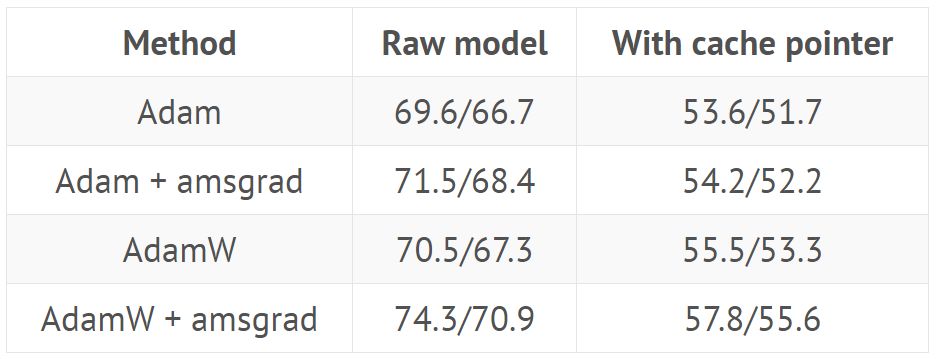
Train QRNN with hyperparameters from GitHub repo (the results show the perplexity of the validation/test set with or without cache pointers):
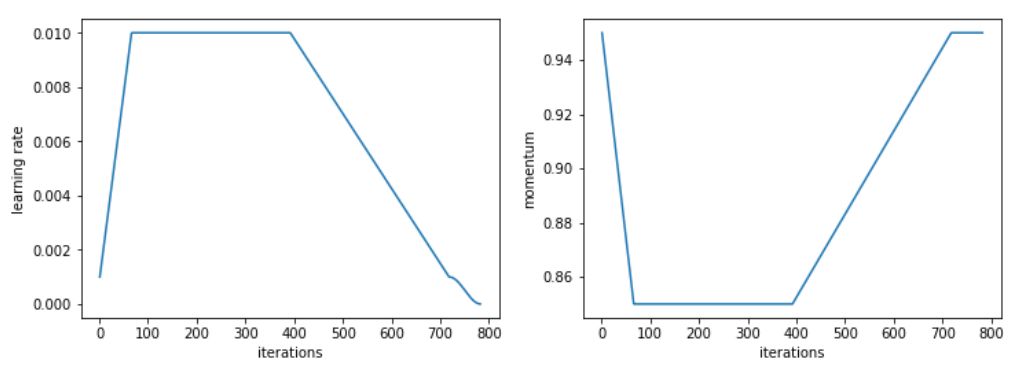
For this specific task, we adopted a modified version of the 1cycle strategy to speed up the learning speed, and then maintain a high constant learning speed for a long time, and then decrease.
Comparison between Adam and other optimizers
Mietubl Global Supply Chain (Guangzhou) Co., Ltd. , https://www.mietublmachine.com