This paper mainly introduces four commonly used wavelet denoising methods, such as wavelet decomposition and reconstruction method, nonlinear wavelet transform threshold method, translation invariant wavelet method and wavelet transform modulus maximum method. They are used to denoise the simulation examples separately, and compare the application, denoising performance, calculation speed and influencing factors of these methods.
The simulation signal Blocks in Matlab software is selected as the original signal, and the signal length (ie, the number of sampling points) is N=2048, as shown in Fig. 1a. Since the signal contains several discontinuous points and singular points, the following methods are used to denoise the Blocks signal (signal-to-noise ratio of 7) superimposed with Gaussian white noise in Figure 1b, which can be clearly compared. Denoising performance of several methods.
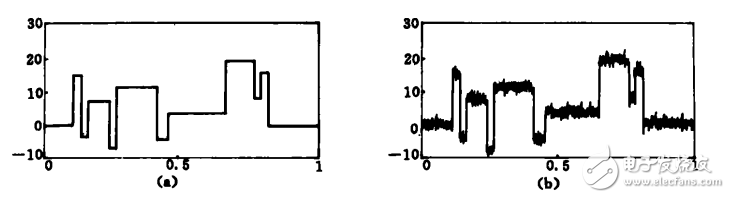
Figure 1 Time domain waveforms of the original signal and the noisy signal
First, wavelet denoising method 1, wavelet decomposition and reconstruction method to denoiseA fast algorithm for wavelet decomposition and reconstruction, namely the Mallet algorithm. According to this algorithm, if fk is the discrete sampled data of the signal f(t), fk=c0,k, then the orthogonal wavelet transform decomposition formula of the signal f(t) is:
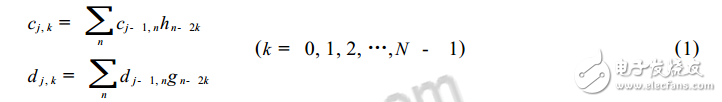
Where cj,k is the scale factor; dj,k is the wavelet coefficient; h, g are a pair of orthogonal image filter banks (QMF); j is the number of decomposition layers; N is the number of discrete sampling points.
The wavelet reconstruction process is the inverse of the decomposition process, and the corresponding reconstruction formula is:
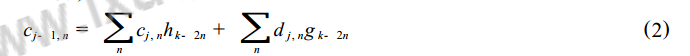
The multi-resolution analysis feature of wavelet transforms the signal at different scales, and decomposes the mixed signals composed of different frequencies into different sub-signals, thus processing the signals by frequency band. ability. The specific steps of denoising using wavelet decomposition and reconstruction are: decomposing the noise-containing signal into different frequency bands at a certain scale as needed, and then zeroing the frequency band in which the noise is located (or directly extracting the useful signal The frequency band) is subjected to wavelet reconstruction to achieve the purpose of denoising.
Figure 2 shows the results of denoising using wavelet decomposition and reconstruction. The wavelet used is an approximately symmetric Symmlet 8 wavelet, and the wavelet decomposition layer number is 4, wherein FIG. 2a is a result of performing 4-layer wavelet decomposition on the noisy signal in FIG. 1b. It can be seen that the energy of the signal is mainly concentrated on a few wavelet coefficients of the low frequency, and the energy of the noise is dispersed throughout the wavelet transform domain. Fig. 2b is a result of extracting the first 256 wavelet coefficients in Fig. 2a for reconstruction, that is, extracting low frequency coefficients and high frequency coefficients on scale 4.
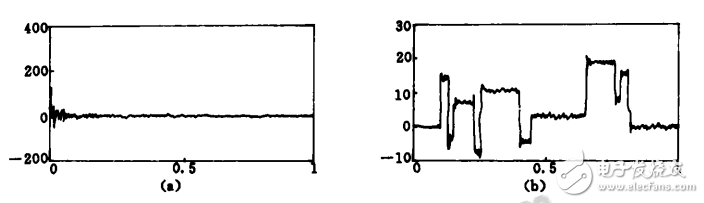
Figure 2 Wavelet decomposition and reconstruction denoising
2. Denoising by nonlinear wavelet transform threshold methodThe nonlinear wavelet transform threshold method is also called "waveletshrinkage", and its denoising method is as follows:
Suppose a finite-length signal superimposed with Gaussian white noise can be expressed as
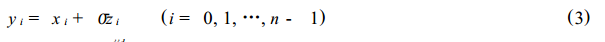
Where zi is a standard Gaussian white noise, ie z ~ N (0, 1), R is the noise level. To recover the original signal xi from the noise-contaminated signal yi, Donoho's denoising method is divided into the following three steps:
(1) Calculate the orthogonal wavelet transform of the noisy signal. Select the appropriate wavelet and wavelet decomposition layer j, and use the (1) formula to decompose the wavelet into the j layer to obtain the corresponding wavelet decomposition coefficient.
(2) Threshold processing of the wavelet coefficients obtained by the decomposition, and there are two methods for processing the threshold:
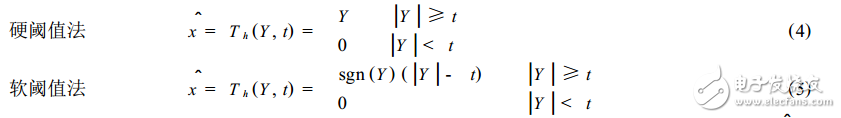
(3) Perform inverse wavelet transform. The threshold-processed wavelet coefficients are reconstructed by equation (2) to obtain the recovered original signal estimate xd.
Wavelet transform has a "concentrated" ability to concentrate the energy of a signal onto a few wavelet coefficients; white noise is in any orthogonal
The transformation on the base is still white noise and has the same magnitude. Relatively speaking, the wavelet coefficient value of the signal is necessarily larger than the wavelet coefficient value of the noise with less energy dispersion and smaller amplitude. Selecting a suitable threshold and thresholding the wavelet coefficients can achieve the purpose of removing noise and retaining useful signals. This method can obtain an approximate optimal estimate of the original signal and has a very wide adaptability.
Figure 3 and Figure 4 show the results obtained by Donoho's nonlinear wavelet transform threshold method and translation invariant wavelet method. Both methods use Haar wavelet, and the number of wavelet decomposition layers is 5. Both use a soft threshold with a threshold size t = 2 log(N), where N is the signal length.

Figure 3 Soft threshold denoising

Figure 4 Translation Invariant Wavelet Method for Denoising
Original Electronics Technology (Suzhou) Co., Ltd. , https://www.original-te.com