introduction
Different equipment interfaces often require different frequencies when transmitting data. On some systems that only use one crystal, if the frequency of one interface is completely matched, the frequency used by other interfaces often does not fully meet the requirements. For example, in order to achieve the 48 MHz transmission frequency of the USB bus, it can generally be obtained by doubling the frequency of the 12 MHz crystal oscillator, and the 12 MHz crystal oscillator does not have a multiple relationship with the standard baud rate during serial communication, so the baud rate is expected. The actual baud rate is often different.
At low baud rates, this error has little effect. For example, when the expected baud rate is 57 600 bps, the actual baud rate is 57 692 bps, the transmission is normal; while when the expected baud rate is as high as 115 200 bps, the actual baud rate is 125 000 bps, the error is larger. The experimental results show that if it is not corrected at this time, the correct transmission cannot be performed.
The author has proved through experimental research that by using the fractional baud rate generator, it can be transmitted correctly as in the case of low baud rate, and the algorithm of fractional approximation of multiple decimal places is realized, which avoids the manual calculation process and completely realizes the wave Automated rate calculation and correction.
1 Working principle of fractional baud rate generator
When the external crystal oscillator or VPB clock value is not an integer multiple of the standard baud rate, the setting of the baud rate tends to deviate. Decimal baud rate generator can reduce or eliminate this deviation.
The following uses the serial port UART1 of the LPC214x processor as an example to illustrate the working principle of the fractional baud rate generator. To use the fractional baud rate generator, you need to set the fractional divider register (U1FDR), which controls the clock divider that generates the baud rate.
The prescaler receives the VPB clock and generates an output clock after a specified fractional number, which is determined by the value of this register.
When the fractional baud rate generator is not used, the UART1 baud rate is calculated by the following formula:
UART1baudrate = PCLK / (16 & TImes; (256 & TImes; U1DLM + U1DLL))
When a decimal baud rate generator is used, it is calculated by the following formula:
UART1baudrate = [PCLK / (16 & TImes; (256 & TImes; U1DLM + U1DLL))] × (MulVal / (MulVal + DivAddVal)
Among them PCLK is VPB bus clock, U1DLM and U1DLL are standard UART1 baud rate divisor registers. It can be seen that MulVal / (MulVal + DivAddVal) is a small value used to correct the baud rate and is called the calibration coefficient. It consists of two parameters: DivAddVal (baud rate generation to divide the value) and MulVal (baud rate prescaler multiplication value). Both DivAddVal and MulVal must be integers and satisfy:
1 ≤ MulVal≤ 15, 0 ≤ DivAddVal ≤ 15.
According to the above formula, it is easy to calculate the serial port baud rate, but in practical applications, it is more to determine the baud rate calibration coefficient when using a non-standard crystal oscillator, that is, to set the values ​​of DivAddVal and MulVal in the U1FDR register. The determination of the baud rate calibration factor can be performed in the following 3 steps:
â‘ Determine the value of the divisor latch: According to the required baud rate bps, determine the value of the divisor latch (DLM, DLL) according to the baud rate calculation formula without calibration coefficients. Due to the use of non-standard crystals, the results obtained are usually decimal. Regardless of the size of the decimal value, the value of the fractional part is discarded, and the result is rounded (not rounded) to obtain the value of the divisor latch.
â‘¡ Determine the baud rate before calibration: Substitute the division value (DLM, DLL) obtained by â‘ into the serial port baud rate calculation formula without calibration coefficients to obtain the uncalibrated baud rate BPS.
â‘¢ Determine the calibration coefficient p: p = bps / BPS = MulVal / (MulVal + DivAddVal)
According to the restriction conditions 1≤MulVal≤15 and 0≤DivAddVal≤15, find a suitable value so that the error is as small as possible.
2 Fractional approximation algorithm for multiple decimal places
(1) The traditional method for obtaining MulVal and DivAddVal integer values
Assuming that the system crystal oscillator is 12 MHz and the baud rate bps is set to 115 200 bps, according to the determination process of the calibration coefficient described above, 12 000 000 / (16 × 115 200) = 6.51, and 6 is the division value, then BPS = 12 000 000 / [16 × (256 × 0 + 6)] = 125 000 bps, so p = bps / BPS = 0.921 6.
The traditional methods for obtaining MulVal and DivAddVal integer values ​​mostly rely on empirical skills or trial and error. As described in Reference 2 "Understanding ARM7LPC214x", page 77:
According to the limits of 1 ≤ MulVal ≤ 15 and 0 ≤ DivAddVal ≤ 15, since the coefficient is close to 1, DivAddVal takes the smallest possible integer. After many tests, the value is 12 / (1 + 12) = 0.9231, which is the closest to the expected coefficient of 0.9216, which can minimize the baud rate error. Therefore, MulVal = 12 and DivAddVal = 1 are finally determined.
Obviously, it is impossible to complete the program automation according to this method, and the values ​​of MulVal and DivAddVal must be manually calculated according to the baud rate before each programming, and a large amount of error comparison and trial and error are required, resulting in a reduction in work efficiency.
(2) New method for obtaining MulVal and DivAddVal integer values
Our problem is to find a score that can be as close to the calibration coefficient as possible. Then you can use such a multi-digit fractional approximation method. The algorithm believes that any multi-digit decimal, whether it is an irrational number or a rational number, can be approximated by a fraction, and a certain program can be used to make the error more and more The smaller, until the required accuracy is achieved.
According to the algorithm, the automatic calculation of these two parameters can be achieved through a program. The program flow is shown in Figure 1.
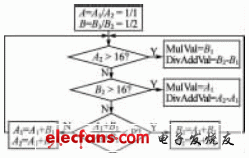
Figure 1 program flow
During initialization, it is required to find the values ​​of A and B so that they satisfy B
Using the restrictions of 1 ≤ MulVal ≤ 15 and 0 ≤ DivAddVal ≤ 15 as the iterative exit conditions, when the denominator of A exceeds 16, B is the optimal solution, B1 is MulVal, and DivAddVal is equal to B2-B1; Similarly, when When the denominator of B exceeds 16, MulVal = A1 and DivAddVal = A2-A1.
In this example, the program calculates MulVal = 12 and DivAddVal = 1, which are completely the same as the manual calculation results. Therefore, using this algorithm, the program can automatically and efficiently calculate MulVal and DivAddVal integer values, which not only saves manpower, but also is more scientific and reliable.
Conclusion
It realizes the purpose of obtaining the setting register parameter value automatically, correctly and quickly by the program, which not only improves the work efficiency, but more importantly, it fully realizes the automation without the need for manual intervention.
Wireless Fence,Wireless Dog Collar,Wireless Dog Fence,Wireless Electric Dog Fence
Elite-tek Electronics Ltd , https://www.aetertek.ca